One After Another: Learning Incremental Skills for a Changing World

Abstract

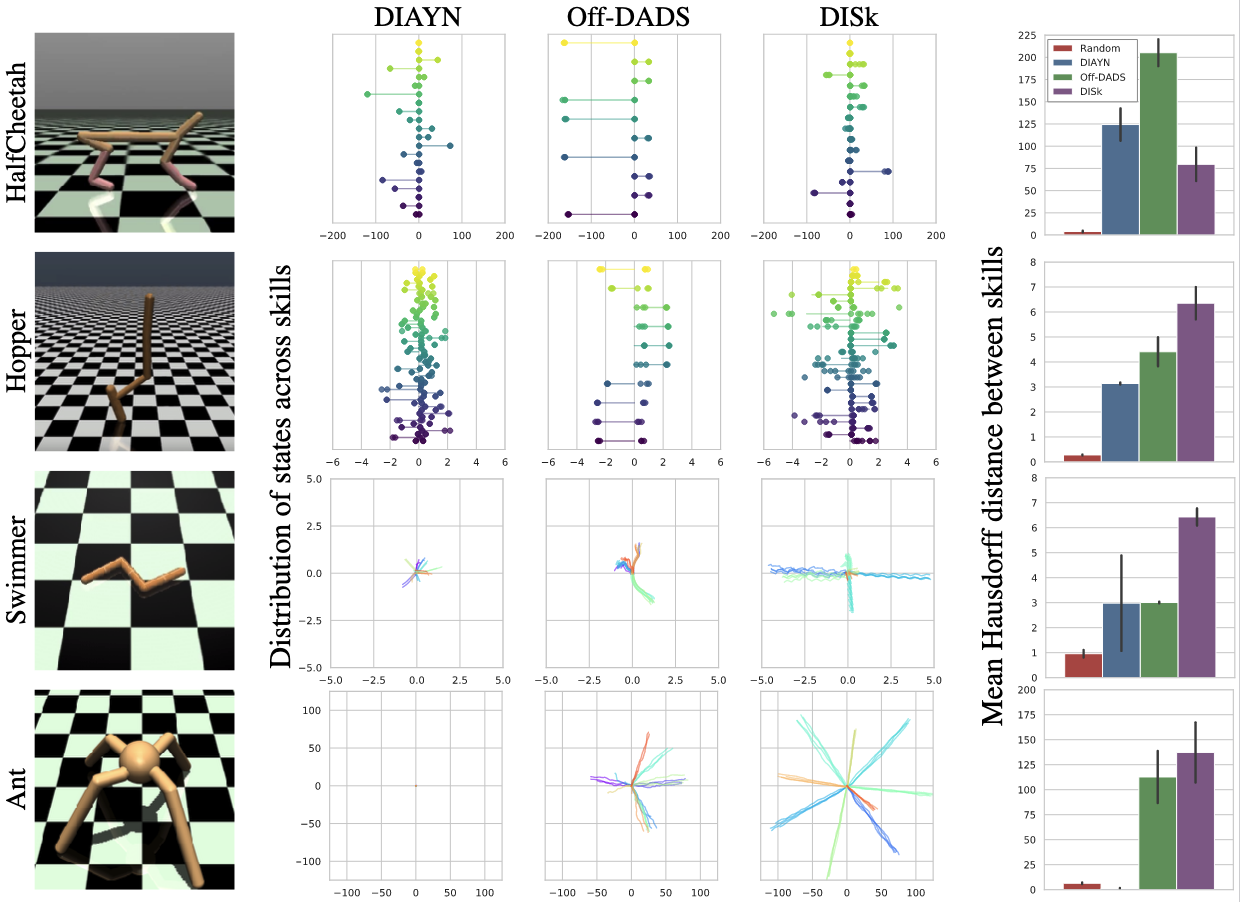
Reward-free, unsupervised discovery of skills is an attractive alternative to the bottleneck of hand-designing rewards in environments where task supervision is scarce or expensive. However, current skill pre-training methods, like many RL techniques, make a fundamental assumption — stationary environments during training. Traditional methods learn all their skills simultaneously, which makes it difficult for them to both quickly adapt to changes in the environment, and to not forget earlier skills after such adaptation. On the other hand, in an evolving or expanding environment, skill learning must be able to adapt fast to new environment situations while not forgetting previously learned skills. These two conditions make it difficult for classic skill discovery to do well in an evolving environment. In this work, we propose a new framework for skill discovery, where skills are learned one after another in an incremental fashion. This framework allows newly learned skills to adapt to new environment or agent dynamics, while the fixed old skills ensure the agent doesn't forget a learned skill. We demonstrate experimentally that in both evolving and static environments, incremental skills significantly outperform current state-of-the-art skill discovery methods on both skill quality and the ability to solve downstream tasks.

Method

The key feature of our algorithm, DISk, is that it learns skills incrementally. This means that, at any time, DISk starts with some previously learned skills, and can learn a new skill that is different from the previous skills while being consistent with itself.

To learn a new skill \(\pi_M\) in a potentially evolved environment, we start with collecting an experience buffer \(\tau\) with states \(s\sim\pi_m\) collected from previous skills. Then, we collect transitions \((s, a, s')\) by running \(\pi_M\) on the environment. We store this transition in the replay buffer, and also store the projected state \(\sigma(s')\)in a circular buffer Buf. Then, to update our policy parameter \(\theta_M\), on each update step, we sample \((s, a, s')\) from our replay buffer and calculate the intrinsic reward of that sample.

To calculate this, we first find the \(k^{\text{th}}\) Nearest Neighbor of \(\sigma(s')\) within Buf, called \(\sigma_c\) henceforth. Then, we sample a batch \(\tau_b \subset \tau\), and find the \(k^{\text{th}}\) Nearest Neighbor of \(\sigma(s')\) within \(\sigma(\tau_b) = \{\sigma(s) \mid s \in \tau_b\}\), called \(\sigma_d\) henceforth. Given these nearest neighbors, we define our consistency penalty $$r_c := ||\sigma(s') - \sigma_c||_2$$ and our diversity reward $$r_d := ||\sigma(s') - \sigma_d||_2$$ which yields an intrinsic reward $$r_I := -\alpha r_c + \beta r_d$$ \(\alpha\) and \(\beta\) are estimated such that the expected value of \(\alpha r_c \) and \( \beta r_d\) are close in magnitude, which is done by using the mean values of \(r_c\) and \(r_d\) from the previous skill \(\pi_{M-1}\).